Objects for representing MCMC output.

Source: R/mcmcarray-object.r

A mcmcarray object is returned by the biips_pimh_samples or biips_pmmh_samples functions to represent MCMC output of a given variable.

A mcmcarray.list object is a named list of mcmcarray objects for different monitored variables.

The methods apply identically to mcmcarray or mcmcarray.list objects and return a named list with the same named members as the input object.

mcmcarray(data = NA, dim = length(data), dimnames = NULL,
  iteration = length(dim), chain = NA, name = "mcmcarray", lower = NULL,
  upper = NULL)

is.mcmcarray(object)

is.mcmcarray.list(object)

# S3 method for mcmcarray
biips_summary(object, probs = c(), order = ifelse(mode,
  0, 1), mode = all(object == as.integer(object)), ...)

# S3 method for mcmcarray.list
biips_summary(object, ...)

# S3 method for mcmcarray
biips_table(x, ...)

# S3 method for mcmcarray
biips_density(x, bw = "nrd0", ...)

biips_hist(x, ...)

# S3 method for mcmcarray
biips_hist(x, main = NULL, xlab = NULL, ...)

# S3 method for mcmcarray.list
biips_table(x, ...)

# S3 method for mcmcarray.list
biips_density(x, bw = "nrd0", ...)

# S3 method for mcmcarray.list
biips_hist(x, main = NULL, xlab = NULL, ...)

# S3 method for mcmcarray
summary(object, ...)

# S3 method for mcmcarray.list
summary(object, ...)

# S3 method for mcmcarray
density(x, ...)

# S3 method for mcmcarray.list
density(x, ...)

# S3 method for mcmcarray
hist(x, ...)

# S3 method for mcmcarray.list
hist(x, ...)

Arguments

data	numerical vector
dim	vector of integers. dimension of the array
dimnames	character vector
iteration	integer. index of the dimension corresponding to iterations of the MCMC.
chain	integer. index of the dimension corresponding to chain of the MCMC.
name	string. variable name
lower	vector of integers. variable lower bound
upper	vector of integers. variable upper bound
object, x	a mcmcarray or mcmcarray.list object.
probs	vector of reals. probability levels in ]0,1[ for quantiles. (default = c())
order	integer. Moment statistics of order below or equal to order are returned. (default = 0 if all the components are discrete variables and 1 otherwise)
mode	logical. Activate computation of the mode, i.e. the most frequent value among the particles. (default = TRUE if all the components are discrete variables and FALSE otherwise)
...	additional arguments to be passed to the default methods. See density, hist, table
bw	either a real with the smoothing bandwidth to be used or a string giving a rule to choose the bandwidth. See bw.nrd. (default='nrd0')
main, xlab	plotting parameters with useful defaults.

Value

The methods apply identically to mcmcarray or mcmcarray.list objects and return a named list with the same named members as the input object.

The mcmcarray function returns an object of class mcmcarray.

The function is.mcmcarray returns TRUE if the object is of class mcmcarray.

The function is.mcmcarray.list returns TRUE if the object is of class mcmcarray.list.

The method biips_summary returns univariate marginal statistics. The output innermost members are objects of class summary.mcmcarray, i.e. lists with members:

mean

mean, if order>=1.

var

variance, if order>=2.

skew

skewness, if order>=3.

kurt

kurtosis, if order>=4.

probs

vector of quantile probabilities.

quant

list of quantile values, if probs is not empty.

mode

most frequent values for discrete components.

The method biips_table returns univariate marginal frequency tables or probability mass estimates of discrete variables. The output innermost members are objects of class table.mcmcarray. The method biips_density returns univariate marginal kernel density estimates. The output innermost members are objects of class density.mcmcarray. The method summary is an alias for biips_summary. The method density is an alias for biips_density. The method hist is an alias for biips_hist.

See also

density

Examples

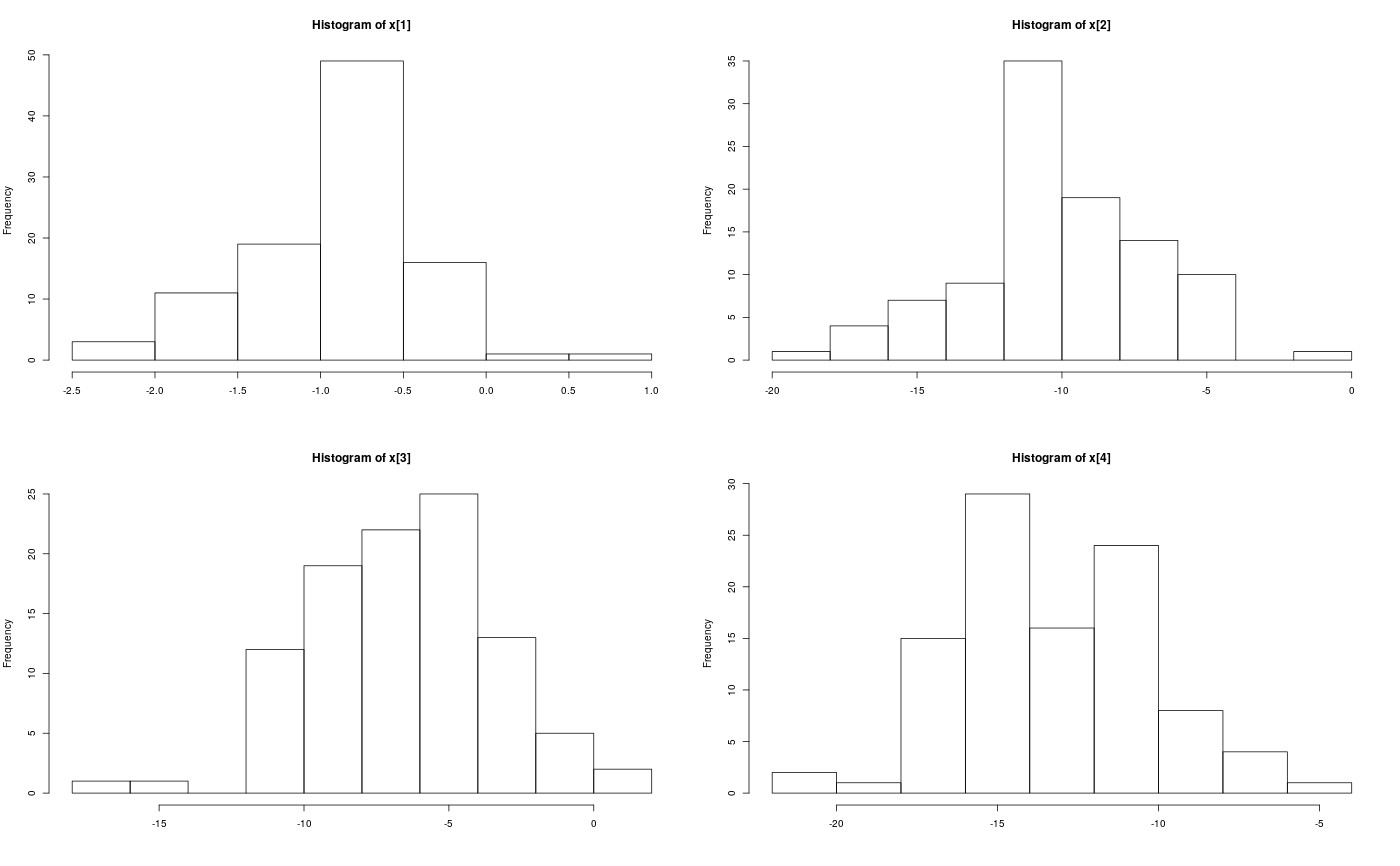
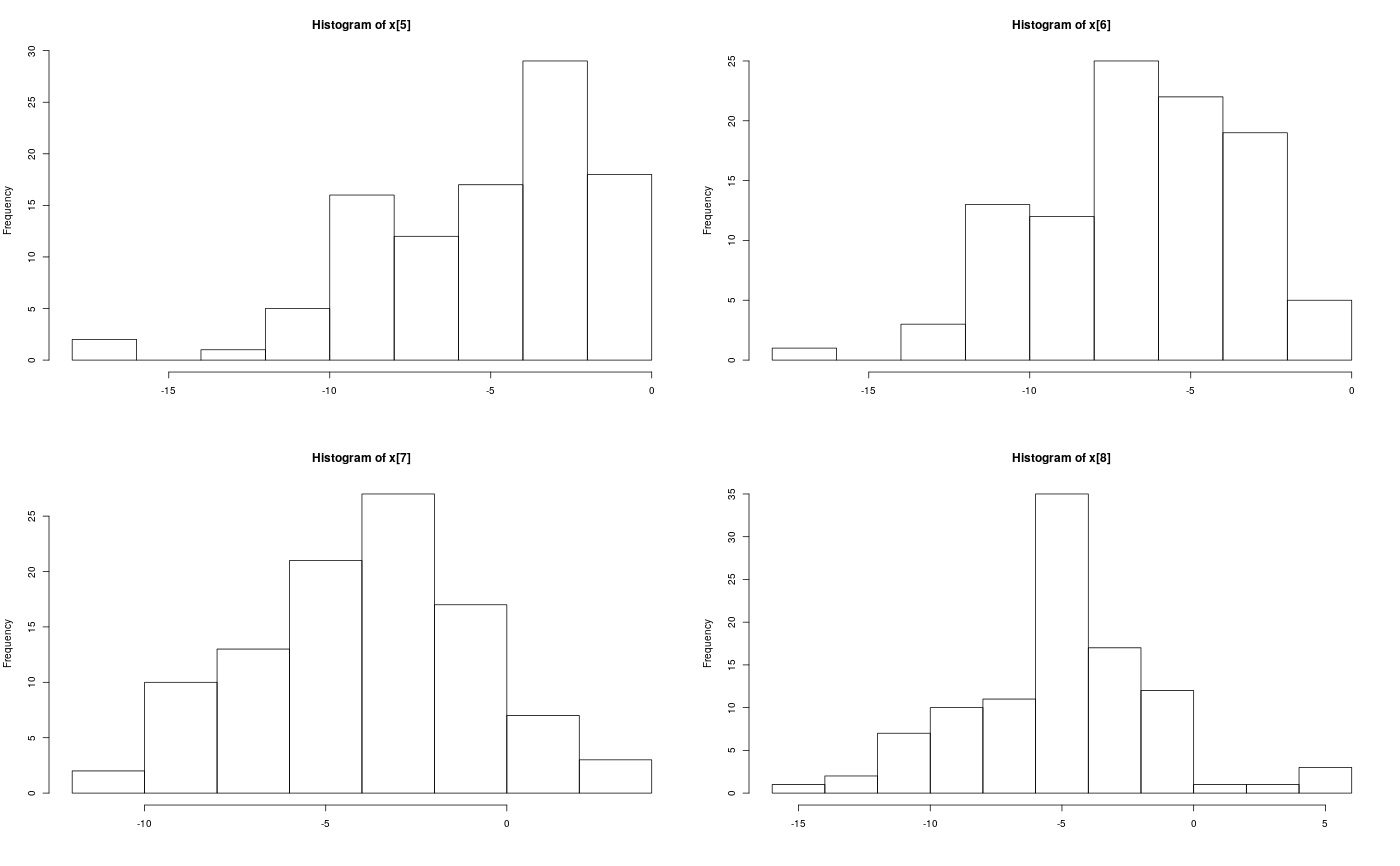
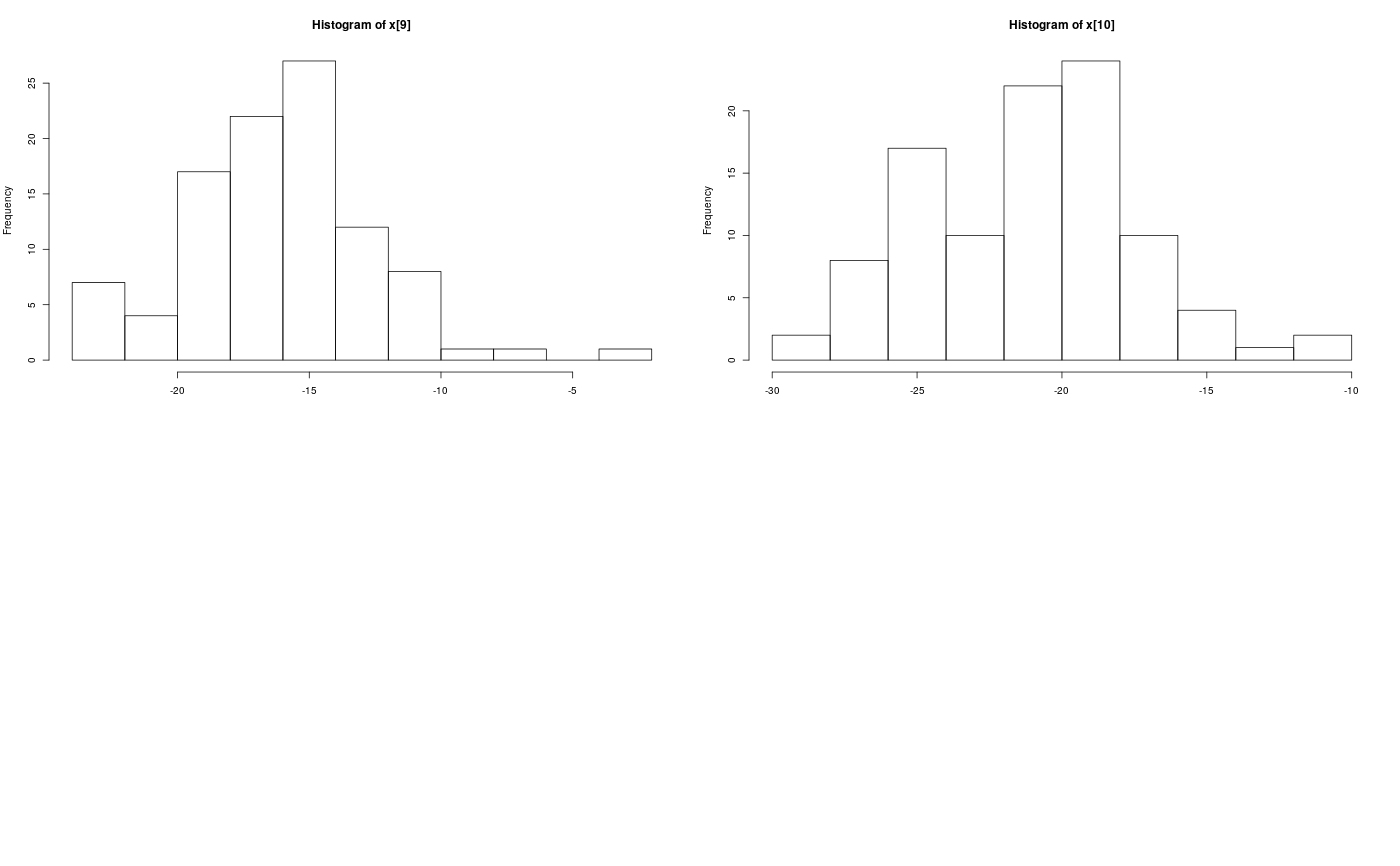
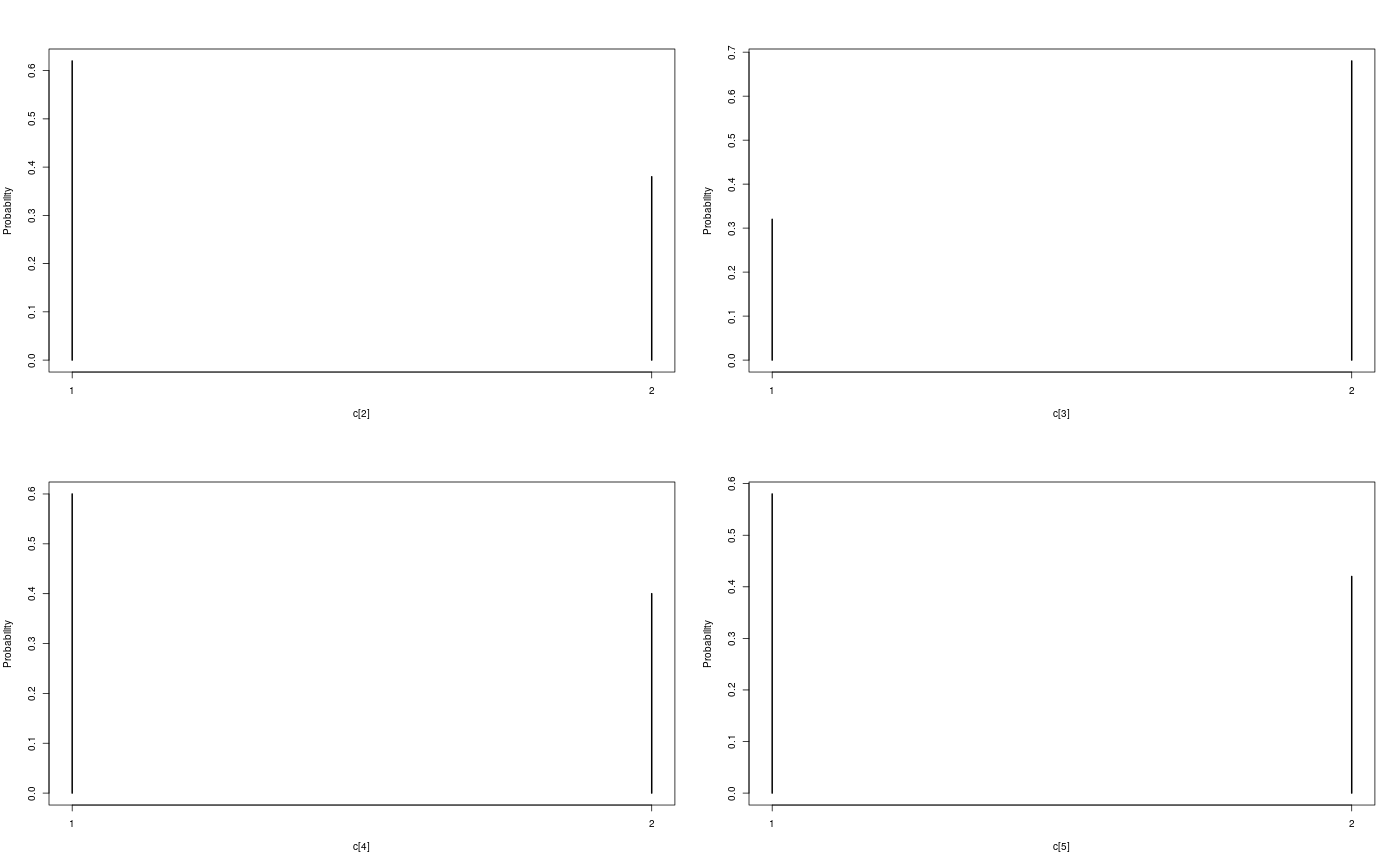
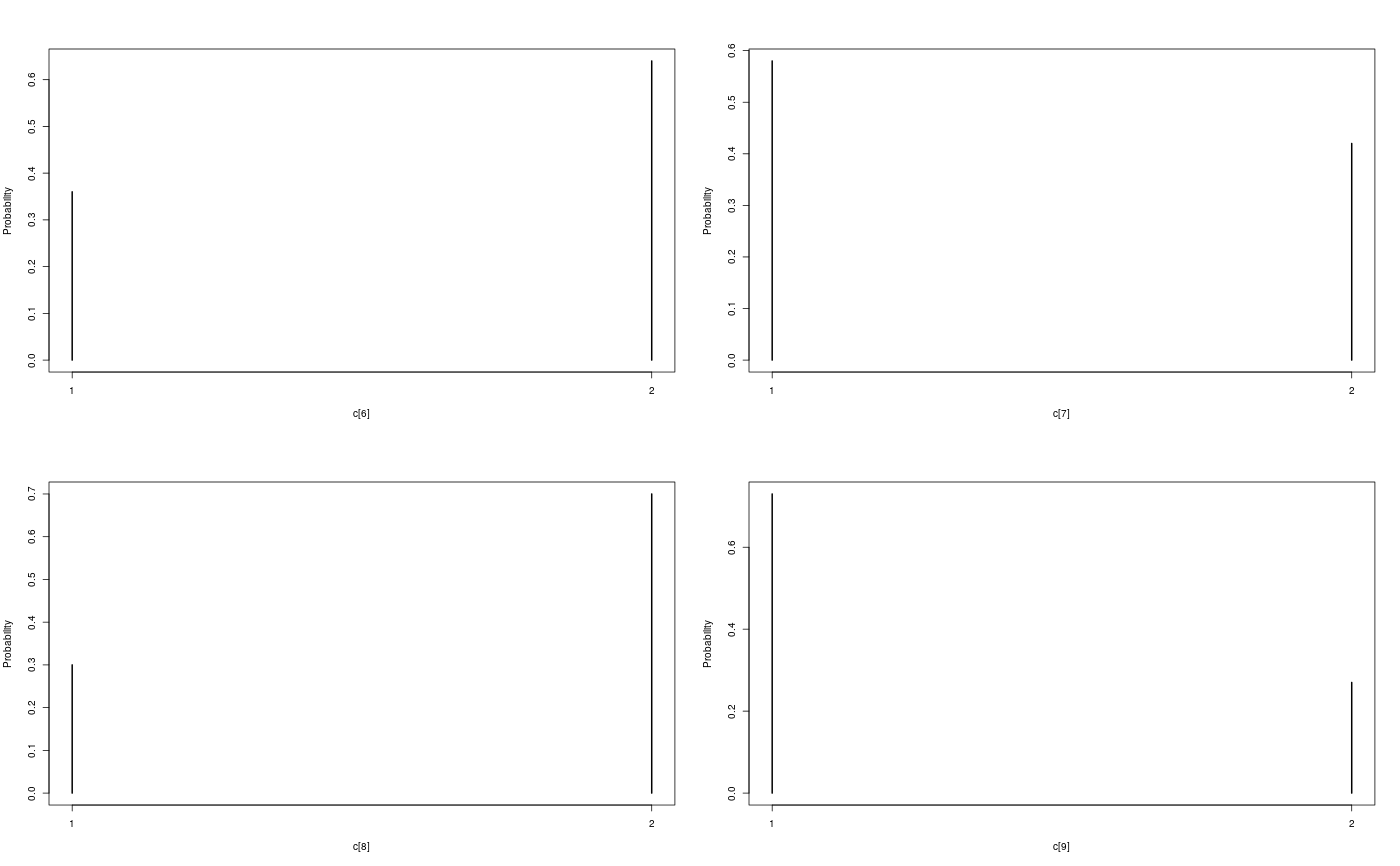
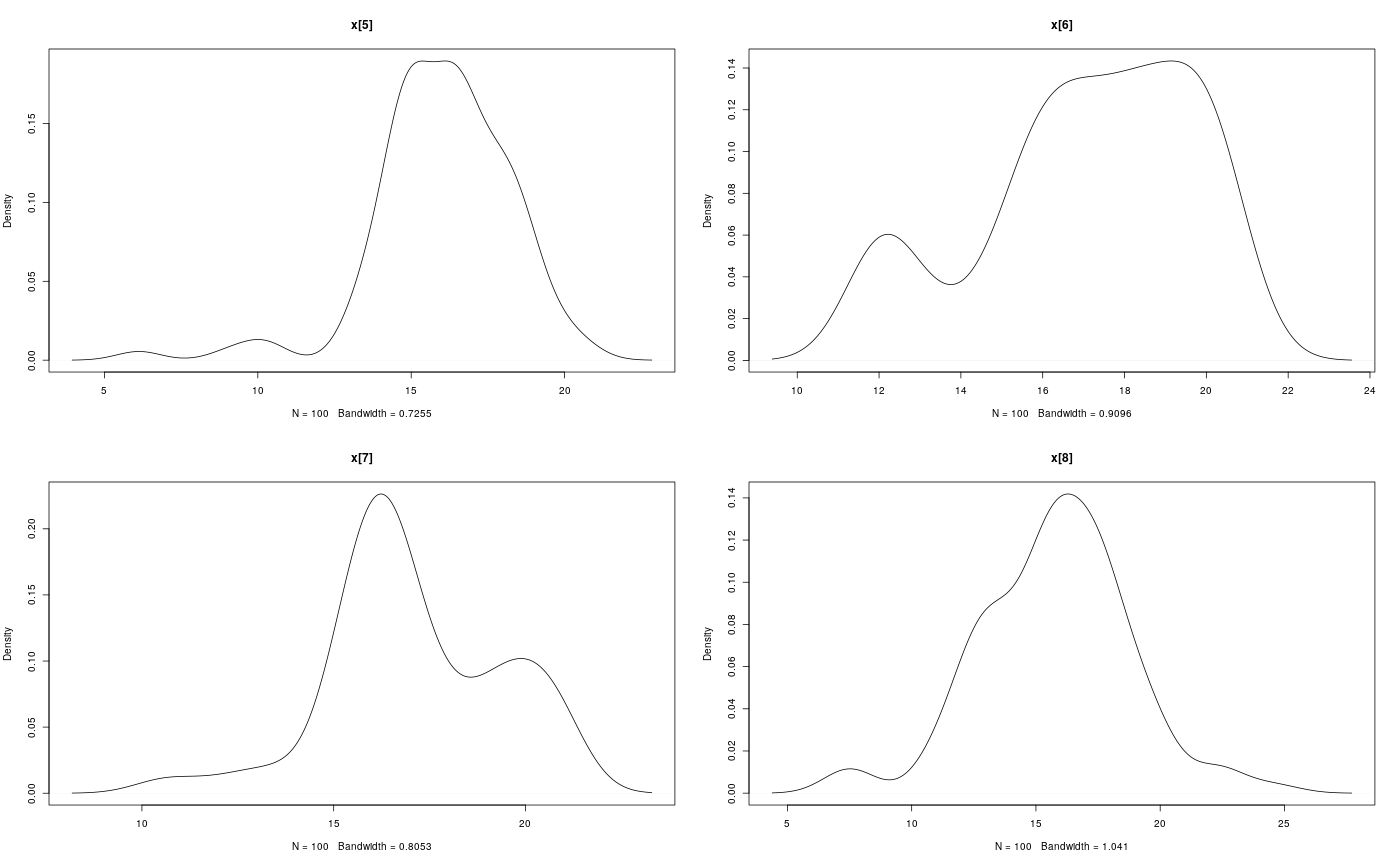
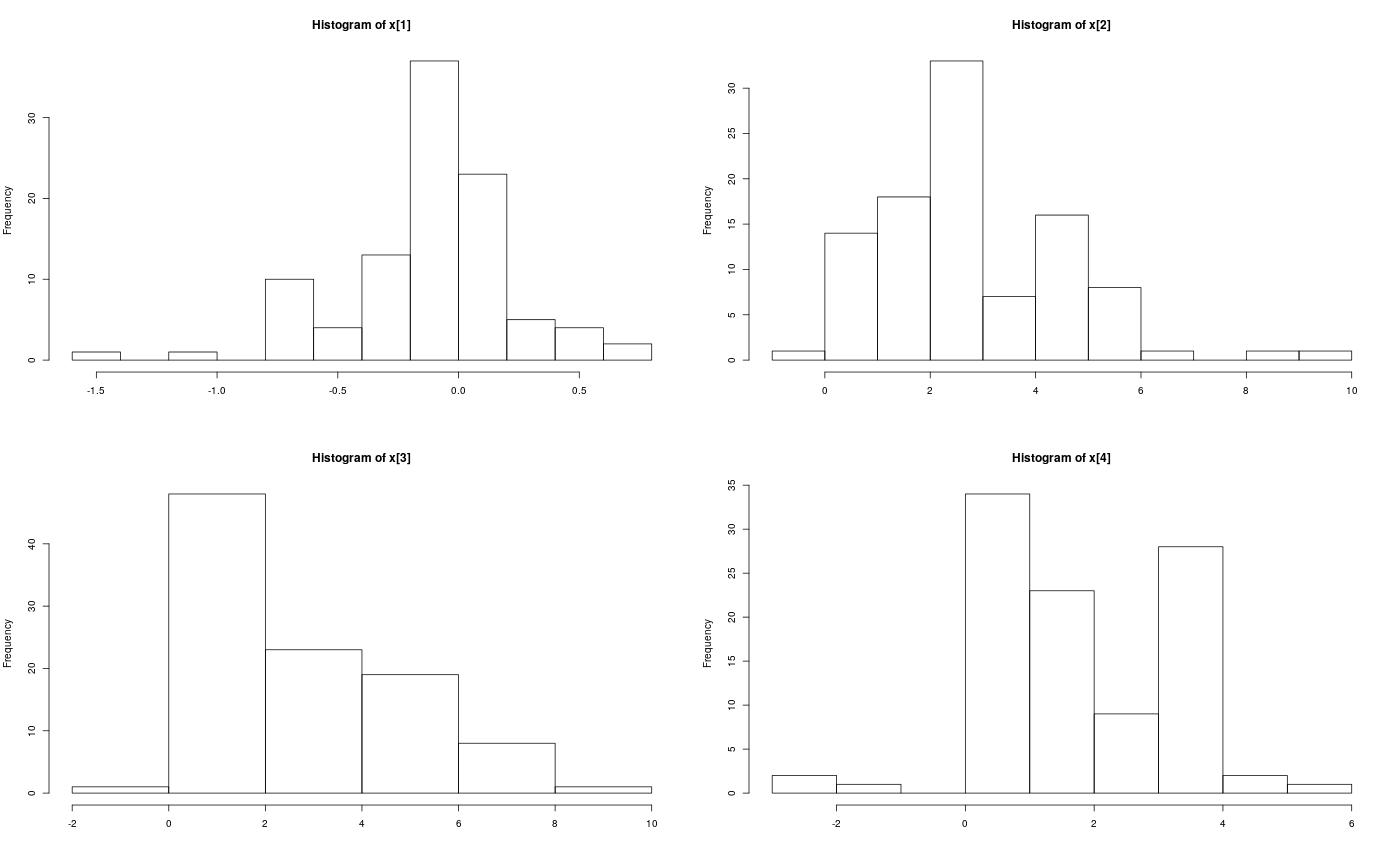
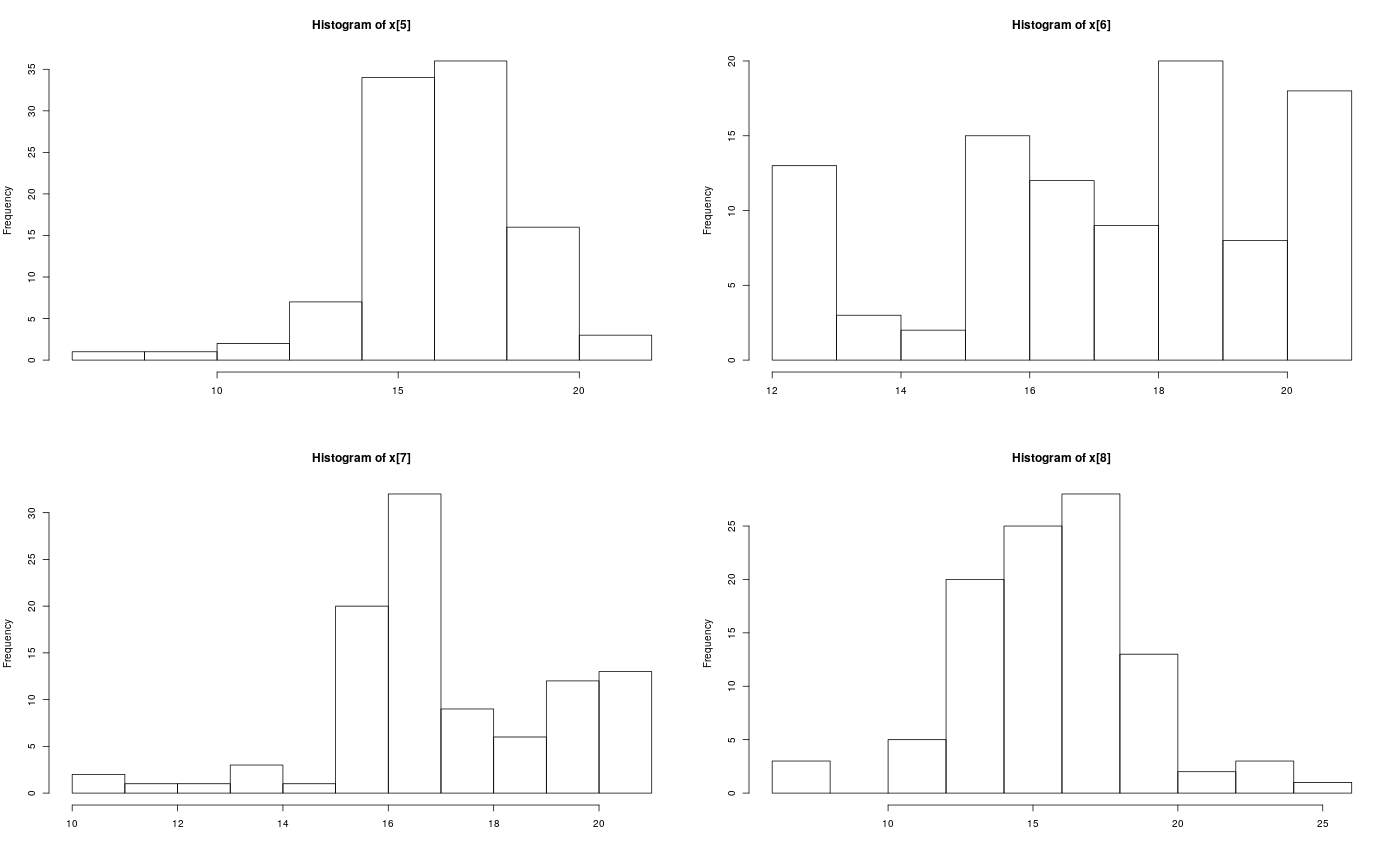
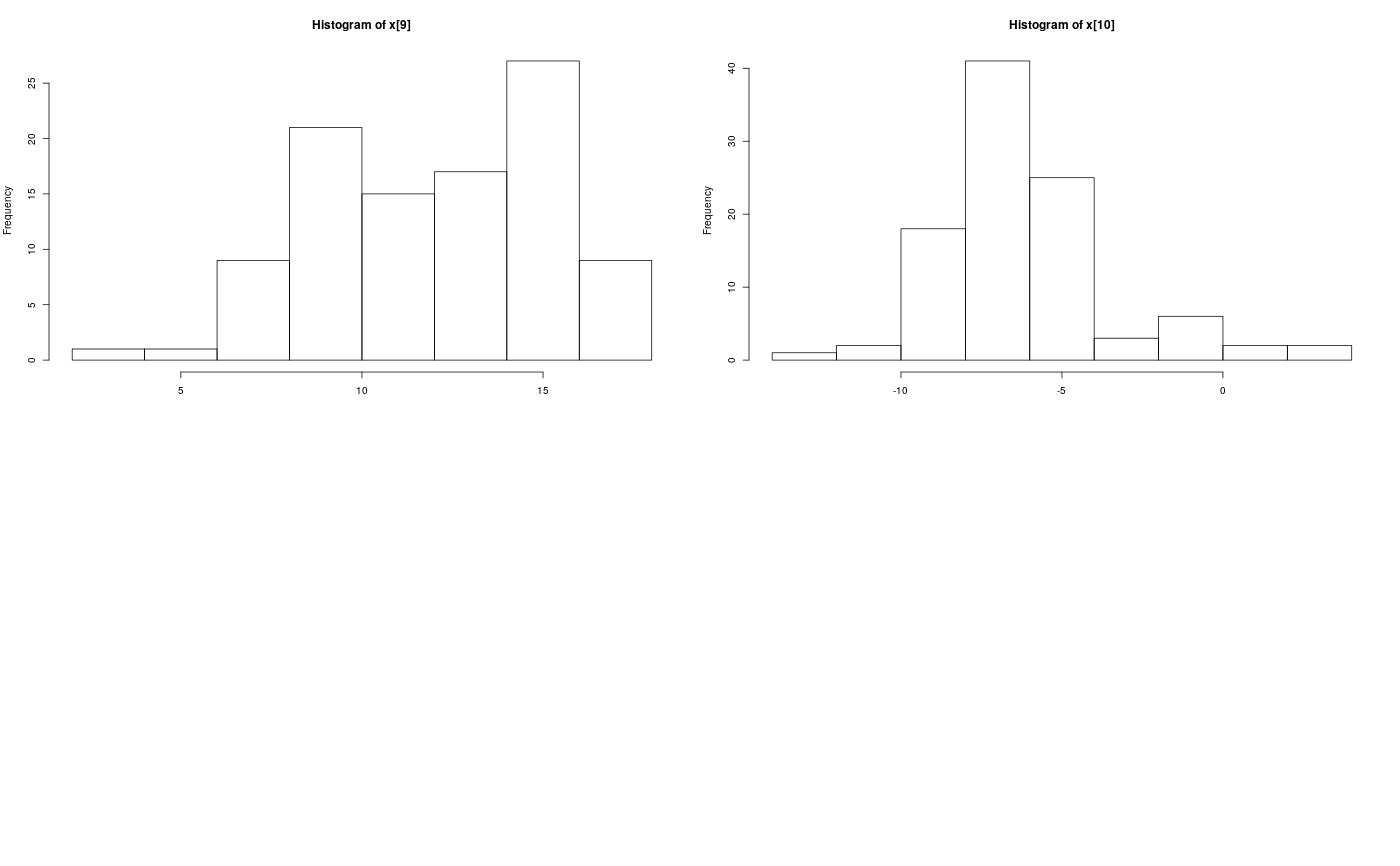
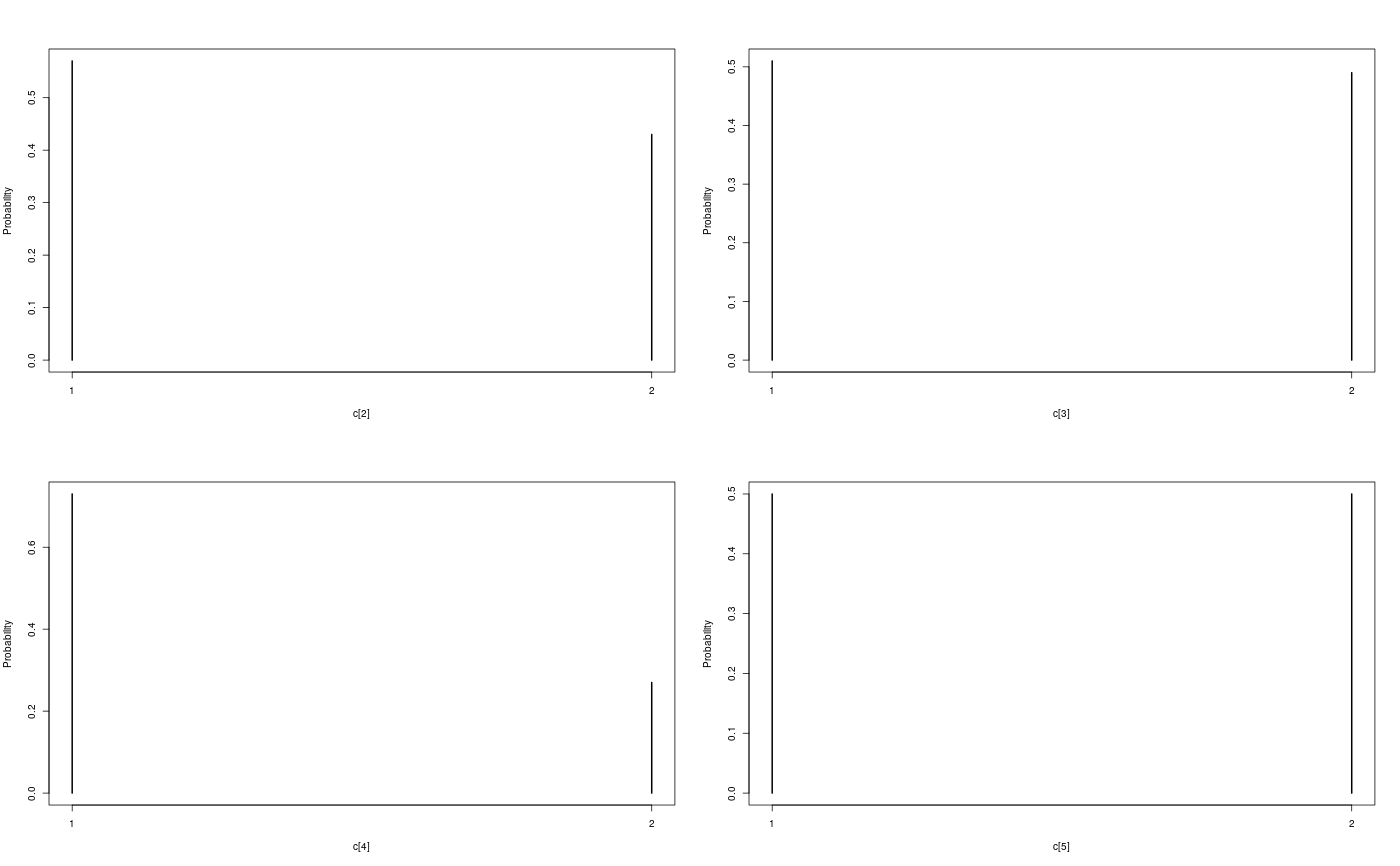
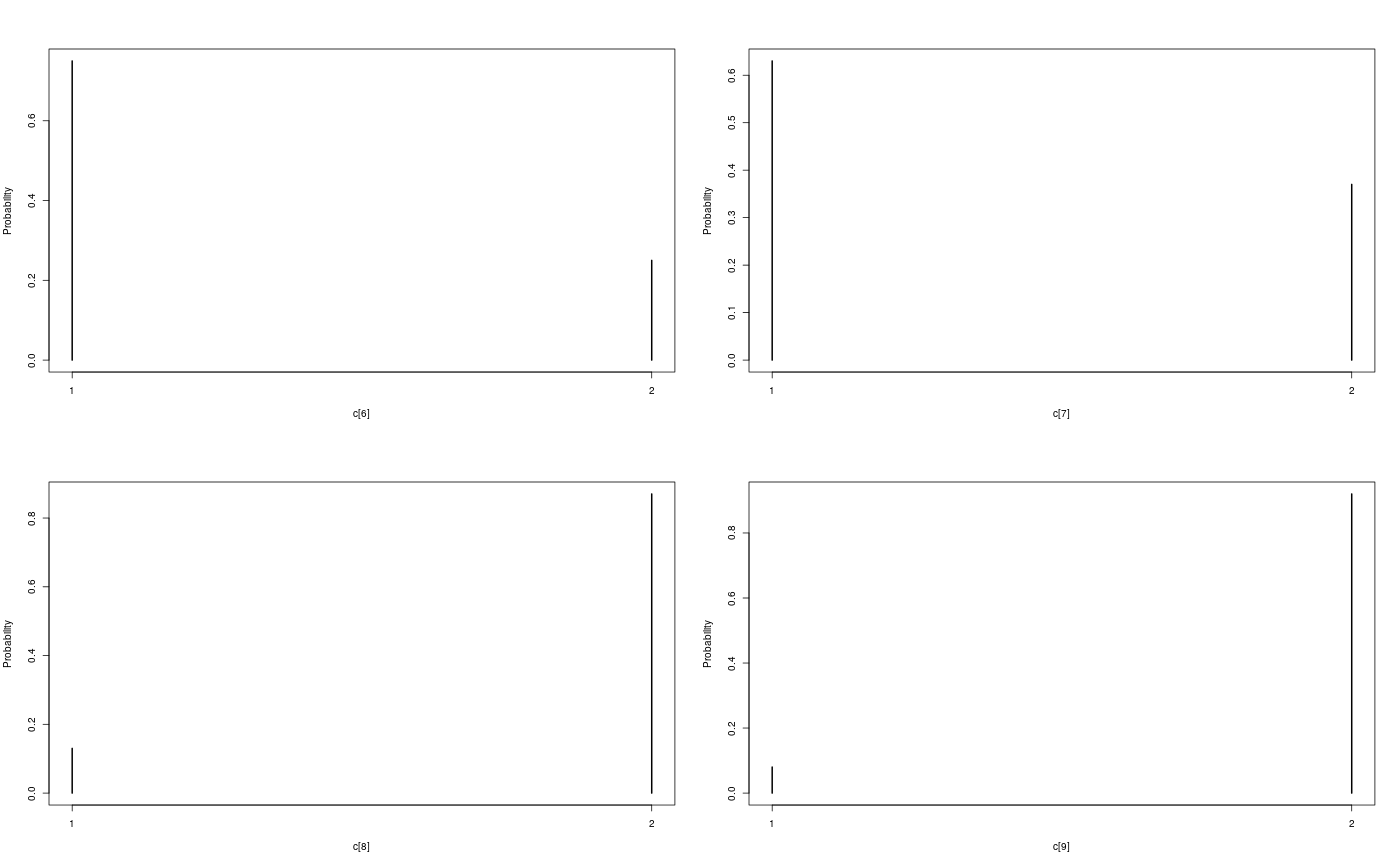
modelfile <- system.file('extdata', 'hmm.bug', package = 'rbiips')
stopifnot(nchar(modelfile) > 0)
cat(readLines(modelfile), sep = '\n')
#> var c_true[tmax], x_true[tmax], c[tmax], x[tmax], y[tmax]
#> 
#> data
#> {
#>   x_true[1] ~ dnorm(0, 1/5)
#>   y[1] ~ dnorm(x_true[1], exp(logtau_true))
#>   for (t in 2:tmax)
#>   {
#>     c_true[t] ~ dcat(p)
#>     x_true[t] ~ dnorm(0.5*x_true[t-1]+25*x_true[t-1]/(1+x_true[t-1]^2)+8*cos(1.2*(t-1)), ifelse(c_true[t]==1, 1/10, 1/100))
#>     y[t] ~ dnorm(x_true[t]/4, exp(logtau_true))
#>   }
#> }
#> 
#> model
#> {
#>   logtau ~ dunif(-3, 3)
#>   x[1] ~ dnorm(0, 1/5)
#>   y[1] ~ dnorm(x[1], exp(logtau))
#>   for (t in 2:tmax)
#>   {
#>     c[t] ~ dcat(p)
#>     x[t] ~ dnorm(0.5*x[t-1]+25*x[t-1]/(1+x[t-1]^2)+8*cos(1.2*(t-1)), ifelse(c[t]==1, 1/10, 1/100))
#>     y[t] ~ dnorm(x[t]/4, exp(logtau))
#>   }
#> }

#' # PIMH algorithm
data <- list(tmax = 10, p = c(.5, .5), logtau_true = log(1), logtau = log(1))
model <- biips_model(modelfile, data, sample_data = TRUE)
#> * Parsing model in: /home/adrien/Dropbox/workspace/rbiips/inst/extdata/hmm.bug
#> * Compiling data graph
#>   Declaring variables
#>   Resolving undeclared variables
#>   Allocating nodes
#>   Graph size: 169
#>   Sampling data
#>   Reading data back into data table
#> * Compiling model graph
#>   Declaring variables
#>   Resolving undeclared variables
#>   Allocating nodes
#>   Graph size: 180

n_part <- 50
obj_pimh <- biips_pimh_init(model, c('x', 'c[2:10]'))  # Initialize
#> * Initializing PIMH
out_pimh_burn <- biips_pimh_update(obj_pimh, 100, n_part)  # Burn-in
#> * Updating PIMH with 50 particles
#>   |--------------------------------------------------| 100%
#>   |**************************************************| 100 iterations in 0.24 s
out_pimh <- biips_pimh_samples(obj_pimh, 100, n_part)  # Samples
#> * Generating PIMH samples with 50 particles
#>   |--------------------------------------------------| 100%
#>   |**************************************************| 100 iterations in 0.25 s

#' Manipulate `mcmcarray.list` object
is.mcmcarray.list(out_pimh)
#> [1] TRUE
names(out_pimh)
#> [1] "log_marg_like" "x"             "c[2:10]"      
out_pimh
#> x mcmcarray:
#> $mean
#>  [1]  -0.9049316 -10.1425908  -6.5297301 -13.3716710  -5.2234602  -6.4363570
#>  [7]  -3.8916198  -5.0545962 -16.0427573 -21.1758321
#> 
#> Marginalizing over: iteration(100) 
#> 
#> c[2:10] mcmcarray:
#> $mode
#> [1] 1 2 1 1 2 1 2 1 2
#> 
#> Marginalizing over: iteration(100) 
#> 
biips_summary(out_pimh)
#> x mcmcarray:
#> $mean
#>  [1]  -0.9049316 -10.1425908  -6.5297301 -13.3716710  -5.2234602  -6.4363570
#>  [7]  -3.8916198  -5.0545962 -16.0427573 -21.1758321
#> 
#> Marginalizing over: iteration(100) 
#> 
#> c[2:10] mcmcarray:
#> $mode
#> [1] 1 2 1 1 2 1 2 1 2
#> 
#> Marginalizing over: iteration(100) 
#> 

#' Manipulate `mcmcarray` object
is.mcmcarray(out_pimh$x)
#> [1] TRUE
out_pimh$x
#> mcmcarray:
#> $mean
#>  [1]  -0.9049316 -10.1425908  -6.5297301 -13.3716710  -5.2234602  -6.4363570
#>  [7]  -3.8916198  -5.0545962 -16.0427573 -21.1758321
#> 
#> Marginalizing over: iteration(100) 
summ_pimh_x <- biips_summary(out_pimh$x, order = 2, probs = c(0.025, 0.975))
summ_pimh_x
#> mcmcarray:
#> $mean
#>  [1]  -0.9049316 -10.1425908  -6.5297301 -13.3716710  -5.2234602  -6.4363570
#>  [7]  -3.8916198  -5.0545962 -16.0427573 -21.1758321
#> 
#> $var
#>  [1]  0.2596974  9.9010249 10.4958097  9.5779322 12.5797948  9.8015063
#>  [7]  9.4897667 13.4860843 11.7294719 13.2027359
#> 
#> $probs
#> [1] 0.025 0.975
#> 
#> $quant
#> $quant$`0.025`
#>  [1]  -1.974696 -16.559188 -11.698147 -18.235634 -12.503916 -12.603412
#>  [7]  -9.159777 -12.086906 -23.625443 -27.277584
#> 
#> $quant$`0.975`
#>  [1]  -0.1075464  -4.5597785  -0.2195797  -7.5721985  -0.5746281  -1.6941463
#>  [7]   2.1248183   3.5768552  -9.8906975 -14.3121566
#> 
#> 
#> Marginalizing over: iteration(100) 
dens_pimh_x <- biips_density(out_pimh$x)
par(mfrow = c(2, 2))
plot(dens_pimh_x)
par(mfrow = c(2, 2))
biips_hist(out_pimh$x)

is.mcmcarray(out_pimh[['c[2:10]']])
#> [1] TRUE
out_pimh[['c[2:10]']]
#> mcmcarray:
#> $mode
#> [1] 1 2 1 1 2 1 2 1 2
#> 
#> Marginalizing over: iteration(100) 
summ_pimh_c <- biips_summary(out_pimh[['c[2:10]']])
summ_pimh_c
#> mcmcarray:
#> $mode
#> [1] 1 2 1 1 2 1 2 1 2
#> 
#> Marginalizing over: iteration(100) 
table_pimh_c <- biips_table(out_pimh[['c[2:10]']])
par(mfrow = c(2, 2))
plot(table_pimh_c)

#' # PMMH algorithm
data <- list(tmax = 10, p = c(.5, .5), logtau_true = log(1))
model <- biips_model(modelfile, data)
#> * Parsing model in: /home/adrien/Dropbox/workspace/rbiips/inst/extdata/hmm.bug
#> * Compiling data graph
#>   Declaring variables
#>   Resolving undeclared variables
#>   Allocating nodes
#>   Graph size: 168
#>   Sampling data
#>   Reading data back into data table
#> * Compiling model graph
#>   Declaring variables
#>   Resolving undeclared variables
#>   Allocating nodes
#>   Graph size: 180

n_part <- 50
obj_pmmh <- biips_pmmh_init(model, 'logtau', latent_names = c('x', 'c[2:10]'),
                            inits = list(logtau = -2))  # Initialize
#> * Initializing PMMH
out_pmmh_burn <- biips_pmmh_update(obj_pmmh, 100, n_part)  # Burn-in
#> * Adapting PMMH with 50 particles
#>   |--------------------------------------------------| 100%
#>   |++++++++++++++++++++++++++++++++++++++++++++++++++| 100 iterations in 0.32 s
out_pmmh <- biips_pmmh_samples(obj_pmmh, 100, n_part, thin = 1)  # Samples
#> * Generating 100 PMMH samples with 50 particles
#>   |--------------------------------------------------| 100%
#>   |**************************************************| 100 iterations in 0.27 s

#' Manipulate `mcmcarray.list` object
is.mcmcarray.list(out_pmmh)
#> [1] TRUE
names(out_pmmh)
#> [1] "log_marg_like_pen" "logtau"            "x"                
#> [4] "c[2:10]"          
out_pmmh
#> logtau mcmcarray:
#> $mean
#> [1] 0.9341417
#> 
#> Marginalizing over: iteration(100) 
#> 
#> x mcmcarray:
#> $mean
#>  [1] -0.1066498  2.8518161  2.8747318  1.7955162 16.0311070 17.1021827
#>  [7] 17.1026065 15.7571541 12.1654708 -6.1548708
#> 
#> Marginalizing over: iteration(100) 
#> 
#> c[2:10] mcmcarray:
#> $mode
#> [1] 1 1 1 1 1 1 2 2 2
#> 
#> Marginalizing over: iteration(100) 
#> 
biips_summary(out_pmmh)
#> logtau mcmcarray:
#> $mean
#> [1] 0.9341417
#> 
#> Marginalizing over: iteration(100) 
#> 
#> x mcmcarray:
#> $mean
#>  [1] -0.1066498  2.8518161  2.8747318  1.7955162 16.0311070 17.1021827
#>  [7] 17.1026065 15.7571541 12.1654708 -6.1548708
#> 
#> Marginalizing over: iteration(100) 
#> 
#> c[2:10] mcmcarray:
#> $mode
#> [1] 1 1 1 1 1 1 2 2 2
#> 
#> Marginalizing over: iteration(100) 
#> 

#' Manipulate `mcmcarray` object
is.mcmcarray(out_pmmh$logtau)
#> [1] TRUE
out_pmmh$logtau
#> mcmcarray:
#> $mean
#> [1] 0.9341417
#> 
#> Marginalizing over: iteration(100) 
summ_pmmh_lt <- biips_summary(out_pmmh$logtau, order = 2, probs = c(0.025, 0.975))
dens_pmmh_lt <- biips_density(out_pmmh$logtau)
par(mfrow = c(2, 1))
plot(dens_pmmh_lt)
biips_hist(out_pmmh$logtau)

is.mcmcarray(out_pmmh$x)
#> [1] TRUE
out_pmmh$x
#> mcmcarray:
#> $mean
#>  [1] -0.1066498  2.8518161  2.8747318  1.7955162 16.0311070 17.1021827
#>  [7] 17.1026065 15.7571541 12.1654708 -6.1548708
#> 
#> Marginalizing over: iteration(100) 
summ_pmmh_x <- biips_summary(out_pmmh$x, order = 2, probs = c(0.025, 0.975))
dens_pmmh_x <- biips_density(out_pmmh$x)
par(mfrow = c(2, 2))
plot(dens_pmmh_x)
par(mfrow = c(2, 2))
biips_hist(out_pmmh$x)

is.mcmcarray(out_pmmh[['c[2:10]']])
#> [1] TRUE
out_pmmh[['c[2:10]']]
#> mcmcarray:
#> $mode
#> [1] 1 1 1 1 1 1 2 2 2
#> 
#> Marginalizing over: iteration(100) 
summ_pmmh_c <- biips_summary(out_pmmh[['c[2:10]']])
table_pmmh_c <- biips_table(out_pmmh[['c[2:10]']])
par(mfrow = c(2, 2))
plot(table_pmmh_c)