Matbiips example: Stochastic kinetic predator-prey model

Reference: R.J. Boys, D.J. Wilkinson and T.B.L. Kirkwood. Bayesian inference for a discretely observed stochastic kinetic model. Statistics and Computing (2008) 18:125-135.

Contents

Statistical model

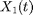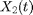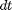The continuous-time Lotka-Volterra Markov jump process describes the evolution of two species $X_{1}(t)$ (prey) and $X_{2}(t)$ (predator) at time $t$. Let $dt$ be an infinitesimal interval. The process evolves as

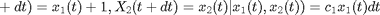
$$\Pr(X_1(t+dt)=x_1(t)+1,X_2(t+dt)=x_2(t)|x_1(t),x_2(t))=c_1x_1(t)dt+o(dt)$$

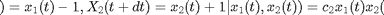
$$\Pr(X_1(t+dt)=x_1(t)-1,X_2(t+dt)=x_2(t)+1|x_1(t),x_2(t))=c_2x_1(t)x_2(t)dt+o(dt)$$

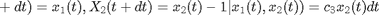
$$\Pr(X_1(t+dt)=x_1(t),X_2(t+dt)=x_2(t)-1|x_1(t),x_2(t))=c_3 x_2(t)dt+o(dt)$$

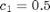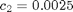where $c_1=0.5$, $c_2=0.0025$ and $c_3=0.3$.

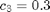Forward simulation can be done using the Gillespie algorithm. We additionally assume that we observe at some time 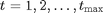$t=1,2,\ldots,t_{\max}$ the number of preys with some noise

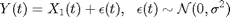
$$ Y(t)=X_1(t) + \epsilon(t), ~~\epsilon(t)\sim\mathcal N(0,\sigma^2) $$

Statistical model in BUGS language

Content of the file 'stoch_kinetic_gill.bug':

model_file = 'stoch_kinetic_gill.bug'; % BUGS model filename
type(model_file);

# Stochastic kinetic predator-prey model
# cf Boys, Wilkinson and Kirkwood
# Bayesian inference for a discretely observed stochastic kinetic model

var x_true[2,t_max], x[2,t_max], y[t_max], c[3]

data
{
  x_true[,1] ~ LV(x_init,c[1],c[2],c[3],1)
  y[1] ~ dnorm(x_true[1,1], 1/sigma^2) 
  for (t in 2:t_max)
  {      
    x_true[1:2, t] ~ LV(x_true[1:2,t-1],c[1],c[2],c[3],1)   
    y[t] ~ dnorm(x_true[1,t], 1/sigma^2)  
  }
}

model
{
  x[,1] ~ LV(x_init,c[1],c[2],c[3],1)
  y[1] ~ dnorm(x[1,1], 1/sigma^2) 
  for (t in 2:t_max)
  {    
    x[,t] ~ LV(x[,t-1],c[1],c[2],c[3],1) 
    y[t] ~ dnorm(x[1,t], 1/sigma^2) 
  }
}

User-defined Matlab functions

Content of the Matlab file 'lotka_volterra_gillepsie.m':

type('lotka_volterra_gillespie.m');

function x = lotka_volterra_gillespie(x, c1, c2, c3, dt)

% Simulation from a Lotka-Volterra model with the Gillepsie algorithm
% x1 is the number of prey
% x2 is the number of predator
% R1: (x1,x2) -> (x1+1,x2)      At rate c1x1
% R2: (x1,x2) -> (x1-1,x2+1)    At rate c2x1x2
% R3: (x1,x2) -> (x1,x2-1)      At rate c3xx2

z = [1, -1, 0;
    0, 1, -1];

t = 0;
while true   
    rate = [c1*x(1), c2*x(1)*x(2), c3*x(2)];
    sum_rate = sum(rate);
    t = t - log(rand)/sum_rate; % Sample next event from an exponential distribution
    ind = find((sum_rate*rand)<=cumsum(rate), 1); % Sample the type of event    
    if t>dt
        break
    end
    x = x + z(:, ind);
end

Content of the Matlab file 'lotka_volterra_dim.m':

type('lotka_volterra_dim.m');

function out_dim = f_dim(x_dim, c1_dim, c2_dim, c3_dim, dt_dim)

out_dim = [2,1];

Installation of Matbiips

  1. Download the latest version of Matbiips
  2. Unzip the archive in some folder
  3. Add the Matbiips folder to the Matlab search path
matbiips_path = '../../matbiips';
addpath(matbiips_path)

General settings

set(0, 'DefaultAxesFontsize', 16);
set(0, 'Defaultlinelinewidth', 2);
set(0, 'DefaultLineMarkerSize', 8);
light_blue = [.7, .7, 1];
light_red = [1, .7, .7];
dark_blue = [0, 0, .5];
dark_red = [.5, 0, 0];

% Set the random numbers generator seed for reproducibility
if isoctave() || verLessThan('matlab', '7.12')
    rand('state', 0)
else
    rng('default')
end

Add new sampler to Biips

Add the user-defined function 'LV' to simulate from the Lotka-Volterra model

fun_bugs = 'LV'; fun_nb_inputs = 5;
fun_dim = 'lotka_volterra_dim'; fun_sample = 'lotka_volterra_gillespie';
biips_add_distribution(fun_bugs, fun_nb_inputs, fun_dim, fun_sample);

* Added distribution 'LV'

Load model and data

Model parameters

t_max = 40;
x_init = [100; 100];
c = [.5, .0025, .3];
sigma = 10;
data = struct('t_max', t_max, 'c', c, 'x_init', x_init, 'sigma', sigma);

Compile BUGS model and sample data

sample_data = true; % Boolean
model = biips_model(model_file, data, 'sample_data', sample_data); % Create Biips model and sample data
data = model.data;

* Parsing model in: stoch_kinetic_gill.bug
* Compiling data graph
  Declaring variables
  Resolving undeclared variables
  Allocating nodes
  Graph size: 131
  Sampling data
  Reading data back into data table
* Compiling model graph
  Declaring variables
  Resolving undeclared variables
  Allocating nodes
  Graph size: 132

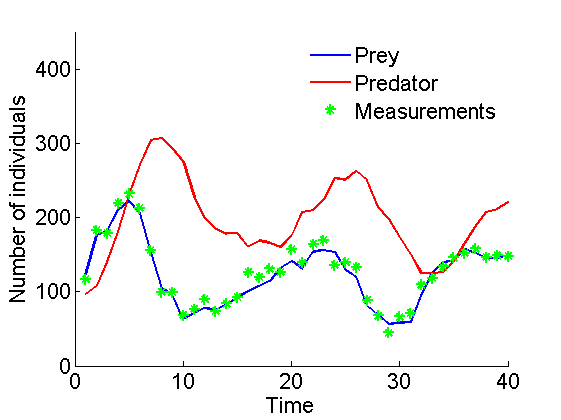
Plot data

figure('name', 'Data')
plot(1:t_max, data.x_true(1,:))
hold on
plot(1:t_max, data.x_true(2,:), 'r')
plot(1:t_max, data.y, 'g*')
xlabel('Time')
ylabel('Number of individuals')
legend('Prey', 'Predator', 'Measurements')
legend boxoff
box off
ylim([0, 450])
saveas(gca, 'kinetic_data', 'epsc2')
saveas(gca, 'kinetic_data', 'png')

Biips Sequential Monte Carlo algorithm

Run SMC

n_part = 10000; % Number of particles
variables = {'x'}; % Variables to be monitored
out_smc = biips_smc_samples(model, variables, n_part, 'type', 'fs');

summ_smc = biips_summary(out_smc, 'probs', [.025, .975]);

* Assigning node samplers
* Running SMC forward sampler with 10000 particles
  |--------------------------------------------------| 100%
  |**************************************************| 40 iterations in 394.67 s

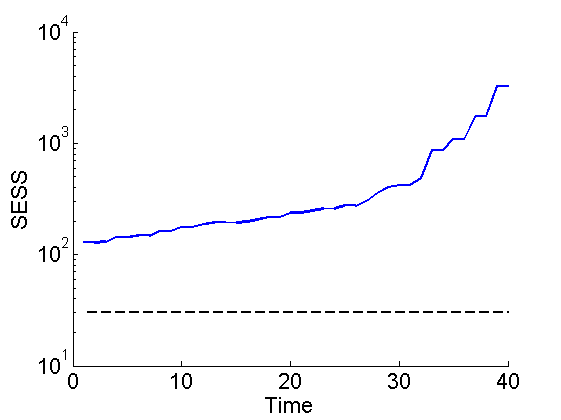
Smoothing ESS

figure('name', 'SMC: SESS')
semilogy(1:t_max, out_smc.x.s.ess(1,:))
hold on
plot(1:t_max, 30*ones(t_max, 1), 'k--')
xlabel('Time')
ylabel('SESS')
box off
ylim([10, n_part])
saveas(gca, 'kinetic_sess', 'epsc2')
saveas(gca, 'kinetic_sess', 'png')

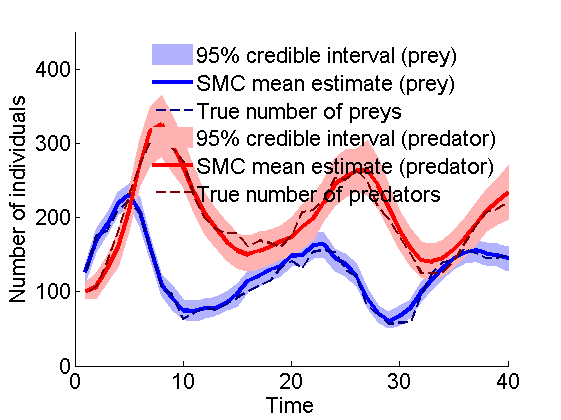
Posterior mean and quantiles for x

figure('name', 'SMC: Posterior mean and quantiles')
x_smc_mean = summ_smc.x.s.mean;
x_smc_quant = summ_smc.x.s.quant;
h = fill([1:t_max, t_max:-1:1], [x_smc_quant{1}(1,:), fliplr(x_smc_quant{2}(1,:))], 0);
set(h, 'edgecolor', 'none', 'facecolor', light_blue)
hold on
plot(1:t_max, x_smc_mean(1, :), 'linewidth', 3)
plot(1:t_max, data.x_true(1,:), '--', 'color', dark_blue)
h = fill([1:t_max, t_max:-1:1], [x_smc_quant{1}(2,:), fliplr(x_smc_quant{2}(2,:))], 0);
set(h, 'edgecolor', 'none', 'facecolor', light_red)
plot(1:t_max, x_smc_mean(2, :), 'r', 'linewidth', 3)
plot(1:t_max, data.x_true(2,:), '--', 'color', dark_red)
xlabel('Time')
ylabel('Number of individuals')
ylim([0, 450])
legend({'95% credible interval (prey)', 'SMC mean estimate (prey)', 'True number of preys',...
    '95% credible interval (predator)', 'SMC mean estimate (predator)',...
    'True number of predators'})
legend boxoff
box off
saveas(gca, 'kinetic_smc', 'epsc2')
saveas(gca, 'kinetic_smc', 'png')

Clear model

biips_clear(model)


Published with MATLAB® R2014a